A coil with an iron core and two aluminum rings are used to demonstrate electromagnetic induction and Lenz’s Law. One of the rings has a slit cut in it, and the other does not (see Figure 3). The rings are placed around the core. When the apparatus is turned on, the solid ring is ejected into the air. The ring with the slit remains. The effect is enhanced if the ring is cooled with liquid nitrogen.
If the button is held down and the ring is dropped from the top of the iron bar, it will remain suspended as shown in Figure 2.
The apparatus also includes a light bulb attached to a small copper coil which shines when the coil is placed around the core and the button is pressed.
Materials:
- Iron core solenoid with push button(see figure 1)
- Solid aluminum ring
- Aluminum ring with slit cut in it(see figure 3)
- Small copper coil with light bulb attached
- Liquid nitrogen for cooling(optional)
Demo:
Place the two aluminum rings around the iron core. Plug the apparatus in and press the button to send current through the coil. The solid ring will eject into the air, while the slitted ring will remain unaffected.
Now remove the rings. Press and hold the button and drop the solid ring from the top of the iron bar. Notice that the ring becomes suspended at an equilibrium position until we release the button, shutting off current flow.
Remove the solid ring again. Place the copper coil with the attached light bulb around the iron bar. Press the button and observe the light bulb shine while we hold the button down.
DO NOT hold the button down for longer than five seconds, as this can heat up the metal or wire significantly and cause burns.
Explanation:

Figure 4 (source)
Faraday’s Law states that any change in a magnetic field about a coil of wire generates an voltage, or emf, about the wire. When we turn our solenoid on, it produces a magnetic field much like a current through a straight wire produces a magnetic field described by the right-hand rule. Using the right hand rule, you can use your thumb to represent the direction of the current and curl your fingers around your imaginary wire. The direction your fingers curl describes the shape of the magnetic field lines in a circle about the wire(see figure 4). A current through a solenoid also produces a magnetic field which can be visualized using figure 5. The strength of this magnetic field depends on the length of the coil, l, and the number of times the wire is looped, n.
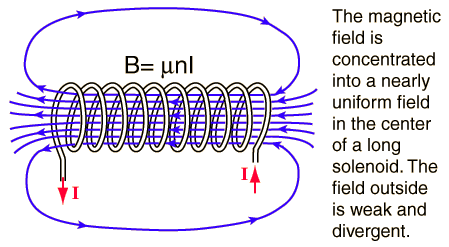
Figure 5 (source)
By turning our solenoid on, the magnetic field around the coil is formed and the change in magnetic environment creates an emf in our aluminum ring or copper wire. This emf induces a current in our aluminum ring that flows in the opposite direction as the current through the solenoid.
We can describe the induced emf mathematically, where:
-
- B = External magnetic field due to solenoid = μnlsolenoid
- A = Area of coil
- Iring = Current through our ring or copper coil
- Φ = BA = Magnetic flux
- n = Number of turns in coil
- ΔΦ/Δt = Change in magnetic flux over time
Using these definitions, the induced emf in our aluminum ring or copper coil is:
Lenz’s Law states that an induced current will always flow in the opposite direction of that which produced it. In other words, the emf induced by the solenoid creates a current in the ring or wire that flows in the opposite direction of the solenoid’s current.
These opposite currents repel one another, as they each create a magnetic force pointing in the opposite direction of one another, causing the aluminum ring to be ejected away from the solenoid. The slitted ring does not eject because an induced current cannot complete a loop around the ring, and remains unaffected by this force. In addition, the copper coil with the light bulb attached is too heavy to be ejected, but we can still observe the induced emf and current via the lit bulb.
When we drop the aluminum ring from above the iron core, the ring stays suspended at some equilibrium position. This equilibrium position is where the magnetic force due to the opposing currents and force due to gravity are exactly equal and opposite, resulting in a ring suspended by these two forces.
Notes:
- DO NOT touch the ring or copper wire while the apparatus is on.
- The use of liquid nitrogen is not needed to produce significant effects, however can be used to make predictions and compare the effects at room temperature versus when cooled.
Written by Lydia Seymour



