Standing waves occur in many natural systems, such as musical instruments, light interference patterns, seismic waves or lasers. The motor driven rubber rope can create 5- 5.5 m long patterns of standing waves of different frequencies. Here, a AC motor driven aluminum wheel is attached to a taut rubber rope and provides reciprocating motion to drive the rubber rope into standing oscillations. This is a good demonstration of harmonic frequencies and standing waves of several orders.
Materials:
- 2 vertical rods
- 2 triple clamps
- C-clamps
- 2 90° rod clamps
- 2 rubber-tipped prong clamps
- Motor with wheel on wooden base
- Variac power supply
- 7m rubber rope
Demo:
- Clamp two metal rods(1) to the side of the desk about 5-6 meters apart using the triple clamps(2). Rods with smaller threading can be screwed directly into the slot or one can use one of the side clamps to hold each rod in place.
- Using C-clamps(3), fasten the board with the motor attached(6) to the table in between the rods so that the motor is attached about 0.5 meters from one rod. Make sure this clamp is tight so that the motor does not get loose from the oscillations.
- Use the 90° rod clamps(4) and rubber-tipped prong clamps(5) to clamp the rubber rope(8) to the two rods(1) and thread it through the loop in the motor. THIS NEEDS TO BE TAUGHT.
- Connect the Veriac power supply(7) to the motor(6) using the banana cables on the motor.
- Power on the power supply(6) and adjust the voltage to achieve a standing wave.
Voltage will convert to frequency through the motor since the aluminum wheel will cause an oscillation at a frequency dependent upon its rotational frequency which is proportional to its voltage. You will need to bring the Variac to a high voltage so that the the motor can begin the oscillation. This will probably cause you to find the 3rd or 4th harmonic before finding the first.

Figure 3
Explanation:
Wave reflection is a common phenomenon and can be easily displayed by sending a pulse down a rope towards a fixed boundary. The reflected wave of this pulse is dependent upon whether the rope is fastened or not. We will refer to a fastened rope as a ‘fixed end’, and an unfastened rope as an ‘free end’. Figure 4 shows a display of the reflection patterns exhibited when sending pulse through a rope of length, L. When the end is fixed, the pulse is inverted and travels in the opposite direction. When the end is free the pulse is not inverted but also travels in the opposite direction.
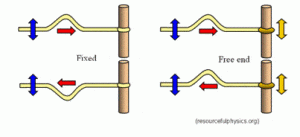
Figure 4: (Left) visual of fixed end reflection. (Right) Visual of free end reflection when sending a pulse through a rope of length, L. http://tap.iop.org/vibration/superposition/page_39882.html
In this demo, we create an environment where there are two fixed ends. Thus, when the first pulse is send down the rope from the motor, it is reflected and inverted. Although, the motor continues to drive more pulses down the rope and therefore the pulses will continue to reflect out of phase and thus the superimposition of these waves will create the standing waves seen in Figure 5. Standing waves are exhibited by the rope when the reflected wave superimposes with the incident wave. If the harmonic frequency is found (the voltage on the Variac when the rope exhibits the first image in Figure 5), we can double this to find the second, third, and fourth harmonics.
Figure 5: Drawing of the first, second and third harmonics (from to top to bottom). http://tap.iop.org/vibration/superposition/page_39882.html
Notes:
- The rope should be taut (no slack) to achieve good patterns of standing waves.
- The 5th harmonic is difficult to find since the rope gets out of control which can damage the demo. Be careful not to turn the voltage too high.
- The rope must be exactly aligned so that the oscillations occur strictly vertically.
- E2-180 is an excellent classroom for this demo.
Written by Phoenix Gallagher

