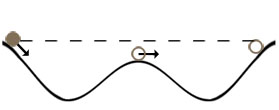
The wave-shaped track represents a system in which total mechanical energy remains the same during the course of motion (Figure 1).
The ends of the track are slightly higher than the middle “hill” part, so the steel ball released from either end rolls down, then over the “hill.” IT reaches almost the same height on the opposite side and returns back.
This track can be used to demonstrate energy transformation, oscillations, roller coasters, “frictionless” motion, role of friction in energy transformation, etc.
Equipment:
- Wave-shaped track
- metal ball
Demo:
Place the metal ball on one of the ends of the track. Release the ball and observe as it rolls over the hill in the center of the track and almost to its original height at the opposite end, then returns back.
Explanation:
Some definitions:
- m = mass of the ball
- v(t) = velocity of the ball at time, t
- h(t) = height of the ball at time, t
In this system there exists kinetic and potential energy. These two energies add to make up the total energy of the system, which remains constant. We may define the kinetic energy as K, the gravitational potential energy as U, and the total energy as E:
K = 1/2mv(t)2
U = mgh(t)
E = K + U
This means that the total energy E, never changes, so as kinetic energy increases, potential energy must decrease, and vice versa. This is also known as energy transformation; potential energy is transformed into kinetic energy as the ball rolls down the track, and kinetic energy is transformed into potential energy as the ball rolls up the track.
Let’s look at the ball various energies the ball will have as it moves along the track:
(1) The ball begins at rest at its maximum height on the edge of the track. The ball is at rest, so its kinetic energy is zero, however it has some height which gives it some gravitational potential energy:
K = 0
U = mghmax
E = mghmax
(2) The ball falls down the first well of the track, having both a non-zero height and velocity. As it loses height and gains speed, gravitational potential energy is transformed into kinetic energy:
K = 1/2mv(t)2
U = mgh(t)
E = 1/2mv(t)2 + mgh(t)
(3) The ball reaches the bottom of the bottom of the first well, hitting a maximum speed and a height of zero:
K = 1/2mvmax2
U = 0
E = 1/2mvmax2
(4) The ball climbs up and down the center hill, where the kinetic and potential energies are both non-zero, as the hill’s height is less than the original height:
K = 1/2mv(t)2
U = mgh(t)
E = 1/2mv(t)2 + mgh(t)
Note that if the ball starts at a height less than the height of the hill at the center of the track, it will not be able to pass the hill, as it would need to have more energy that it started with! In that case, it would oscillate within the first well of the track until it loses all of its kinetic energy to friction.
(5) The ball repeats step (3)
(6) The ball climbs up the last hill, transforming kinetic energy into potential energy as it rises:
K = 1/2mv(t)2
U = mgh(t)
(7) The ball reaches its original height on the other side of the track, where its velocity is zero. The force of gravity will pull the ball back down the track and repeat this process:
K = 0
U = mghmax
E = mghmax
Notice that all of the total energies in each step are equivalent, as energy is conserved.
In a frictionless system, the ball would oscillate forever, always reaching its original height at each end. In our case the ball doesn’t quite reach its maximum height and will eventually come to rest, as some kinetic energy is lost due to friction between the ball and the rail.
Written by Lydia Seymour