Figure 1

Figure 2

A coffee cup on a hanging platform is swung vertically to demonstrate centripetal forces. The liquid remains inside the cup throughout the rotational cycle.

Materials:

• Hanging platform
• Cup filled with liquid

Demo:

Hold the hanging platform by the loop at the top of the apparatus such that the platform hangs parallel to the ground (Figure 1). Carefully set the filled cup on the platform, then swing the platform vertically, in a circular motion (Figure 2). Notice both the cup and the liquid stay in place as the platform makes a full rotation.

Explanation:

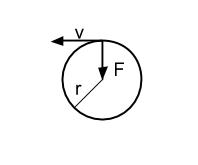
Both the cup and liquid stay in place throughout the entire rotation due to the centripetal force, pointing from the center of mass of the combined platform and cup to the center of rotation (the demonstrator’s hand, in this case). The magnitude of the centripetal force can be described by:

F = mv²/r

Where m is the mass of the combined platform and filled cup, r is the radius of rotation extending from the demonstrator’s hand to the platform, and v is the velocity of the cup pointing tangent to the rotational path. If we were to suddenly stop the motion of the platform, the cup would fly off with this velocity tangent to its original path (Figure 3).

Figure 3

Once the cup starts spinning, however, the centripetal motion exerts force towards the center of rotation, perpendicular to the direction of the cup’s velocity.

Now let’s consider why the water and cup stay in place during rotation. A filled cup turned upside-down will spill its contents due to the gravitational force, so why does our liquid stay in the cup, even with the cup is at the top of its trajectory?

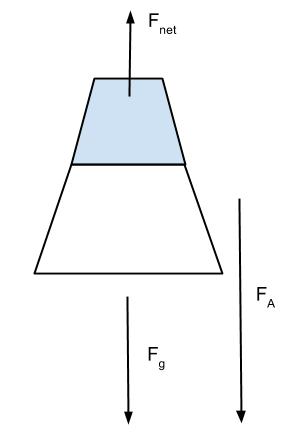
First of all, imagine that we turn over a filled cup and release the cup and its contents. Gravity will pull the cup and the liquid inside at the same acceleration, g. In addition, if we were to turn over the filled cup and slowly move the cup towards the ground at a rate slower than g, the liquid would reach the ground first at a rate of g. If we flip the cup and then pull it down with a rate faster than g, there will be a net force on the liquid, pushing it against the base of the cup(figure 4). This net force is equivalent to the difference between the applied force and the gravitational force.

Figure 4

This example is similar to our demo. In our case, we are spinning the cup fast enough that the applied force (in this case due to the tension in the string) overcomes the gravitational force, and a net force(the difference between these two forces) pushes the liquid to the base of the cup as it rotates on the platform.

This means that if we do not spin the cup fast enough, the gravitational force will overcome the force due to the tension in the string and cause the filled cup to fall off of the platform.

Note:

Practice is recommended before demonstrating in front of an audience.

Written by Lydia Seymour