The Rotating Stool and Dumbbells demonstration shows conservation of angular momentum as a student sits on a rotating stool and moves weights in each hand toward and away from his or her body. The audience will see the increase and decrease in the rotational speed of the stool-body system — a convincing demonstration of the conservation of angular momentum.
The Rotating Stool and Bicycle Wheel is another demonstration of conservation of angular momentum. The gyroscopic properties of the bicycle wheel can be shown with the help of a student sitting on the rotating stool with the spinning bicycle wheel in his or her hands. The stool will begin to rotate when the student tilts the bicycle axle. The audience will see how angular momentum can be transferred inside the system.
Equipment:
- Rotating stool
- Dumbbells(5 lbs each)
- Bicycle Wheel
Demo:
Ask a student to sit on the stool and keep a dumbbell in each hand. Spin the stool and then ask the student to move the weights in and out slowly toward and away from his or her body. Observe the increase or decrease in rotational speed of the stool-body system as the weights are moved towards or away from the student’s body, respectively(Figures 1 and 2).
Now have the student hold a bicycle wheel with the axis of the wheel vertical. With the stool stationary, spin the bicycle wheel and ask the student to tilt the axle. The stool will start spinning in the direction opposite that the wheel spins(Figures 3 and 4).
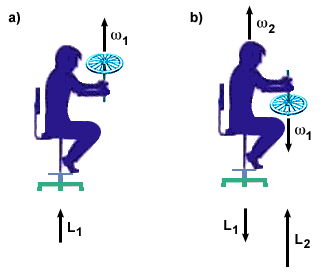
Figure 4(Source)
Explanation:
The student, the stool, and the weights all possess angular momentum and a moment of inertia, but for the purposes of simplicity we will concern ourselves only with the weights. The angular momentum of the weights is
L = Iω ,
where ω is angular velocity, and I is moment of inertia. With the student holding the weights on the rotating stool, their moment of inertia in this case can be described by
I = 1/2mr2 ,
where m is the total mass of the weights and r is the radius extending out from the axis of rotation (the vertical line going through the center of the stool) to the weights in the student’s hands.
As we change the radius by having the student move the weights toward or away from his or her body, the angular velocity must change in order to satisfy conservation of angular momentum in the system. That is, the initial angular momentum must be equal to the final angular momentum – no matter what the position of the weights are relative to the radius, the angular momentum must remain the same.
Mathematically we can see that the angular velocity is inversely proportional to r-squared:
ω ∝ 1/r2
In other words, the angular velocity must increase as the student pulls the weights in, and decrease as the student pushes the weights out.
Now let’s consider the case with the bicycle wheel. This can also be described using conservation of angular momentum.
As the bicycle wheel spins, its angular momentum, L, points along the rotational axis of the wheel(along the wheel’s axle). We can use the right-hand rule to figure out which direction L is pointing: curl the fingers of your right hand along the direction of the spinning wheel (clockwise or counter-clockwise). Your thumb will point along the direction of L.
The Wonders of Physics has a great explanation for why the student begins turning in the opposite direction that the wheel spins. The alternate setup described has the student start with the wheel’s rotational axis horizontal, and turn it 90 degrees to vertical.
“In this demonstration, there are two possible turning motions. The platform the person stands on turns like a wheel on its side. Call this horizontal turning motion. The other turning motion is the bicycle wheel the person is holding. Initially it is vertical, as a bicycle wheel normally stands. Call this vertical turning motion.”
To begin with, someone spins the bicycle wheel. There is vertical turning motion in the bicycle wheel, but no horizontal turning motion of the platform. Then the person tilts the bicycle wheel to the side, so now there is horizontal turning motion where there wasn’t any before. Conservation of angular momentum tries to fix this. The platform starts spinning in the direction opposite that of the bicycle wheel. If you add the backward turning of the platform and the forward turning of the bike wheel together, you get zero. So horizontal motion is the same as when we started: nothing. When the bike wheel is tilted back vertically, the platform stops spinning, as in the beginning.”
Written by Lydia Seymour


