Inclined Plane with Cylinders

 inc_plane

Equipment:

  • Hollow and solid cylinders of same dimensions
  • Solid copper cylinder, solid aluminum cylinder, hollow cylinder partially filled with sand, and a hollow cylinder of the same dimension
  • Also available are three balls: one of solid steel, one of hollow steel, and one of solid aluminum
  • Wide wooden plank
  • Lab jack(s) — depends on the width of the wooden plank
  • Sandbags

Demo:

We have two sets of cylinders for demonstrations. The first set consists of two black cylinders of similar mass and diameter, but one is hollow and the other is solid. When released simultaneously from the top of the incline plane, the solid cylinder quickly takes the lead over the hollow cylinder (see video above). Another set of cylinders has equal dimensions but different masses and moments of inertia; two are solid, one is partially filled with sand, and the fourth is hollow. The two solid cylinders have differing masses, but will have the same final velocity, since their moment of inertia is the same. Both solid cylinders will roll faster than the cylinder partially filled with sand and the hollow cylinder. Furthermore, we also have a set of three spheres; one of solid steel, one of solid aluminum, and one of hollow steel. Once again, the two solid spheres will have a greater final velocity than that of their hollow counterpart.

Explanation:

The energy of the system must be conserved. This means that the potential energy of the cylinder when it is initially at the top of the plane (at point h) must be equal to the total kinetic energy it accumulates when it reaches the end of the ramp; this includes both translational and rotational kinetic energies. 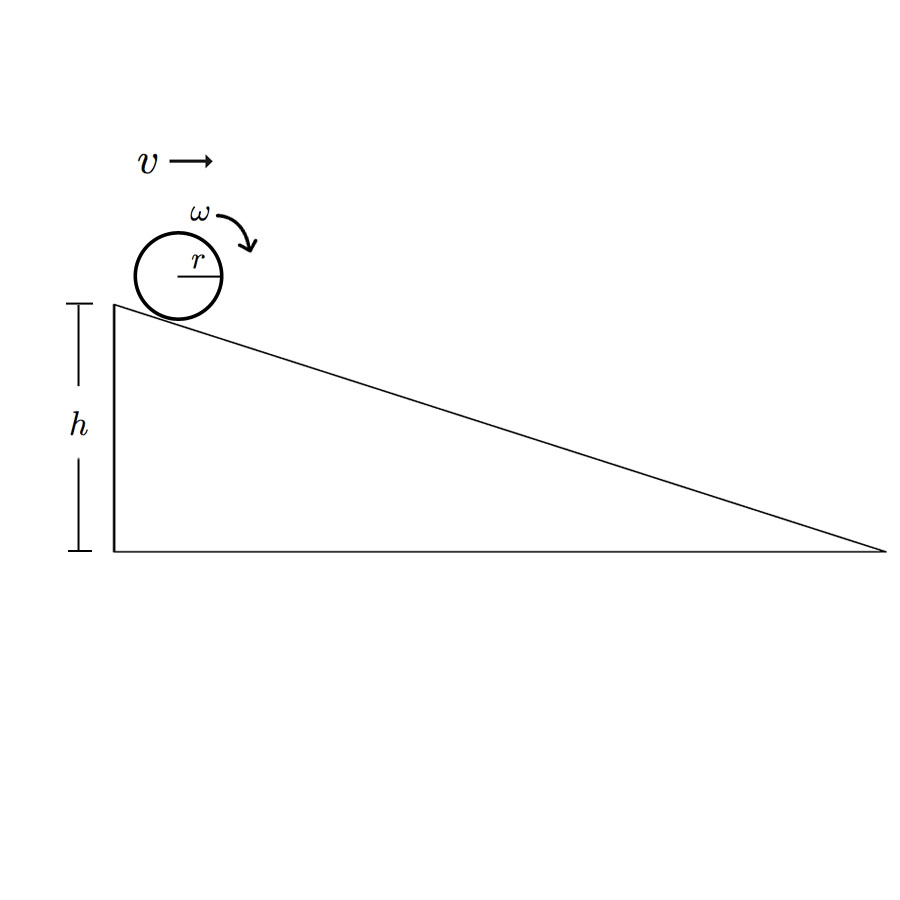RollingCylinder

If the potential energy is given as PE = mgh, the translational kinetic energy as 1/2mv2 and the rotational kinetic energy as 1/2Iω2, then we have conservation of energy expressed as:

mgh = \cfrac{1}{2}mv^2 + \cfrac{1}{2}I\omega^2

For a solid cylinder, the moment of inertia, I, is known to be I = 1/2mr2, while a hollow cylinder has I = mr2. Knowing that angular velocity is related to translational by ω = v/r, we may then compare the final velocities of each object.

For the hollow cylinder, the equation for the conservation of energy becomes:

mgh = \cfrac{1}{2}mv^2 + \cfrac{1}{2}I\cfrac{v^2}{r^2}

= \cfrac{1}{2}mv^2 + \cfrac{1}{2}mr^2\cfrac{v^2}{r^2}

= mv^2

Solving for v gives: v = (gh)1/2.

For the solid cylinder, conservation of energy give s:

mgh = 1/2mv2 + 1/2I(v2/r2)

= 1/2mv2 + 1/4mr2(v2/r2)

= 3/4mv2

Solving for v gives: v = (4gh/3)1/2

Thus, the final velocity of the solid cylinder is greater. The final velocity is dependent on the object’s moment of inertia, not its mass.

The same logic applies to the second set of cylinders; solid cylinders will have a greater final velocity than a cylinder that is not completely solid.

The same concept is applicable to the spheres available for the demonstration; the energy of the system still must be conserved; the equation only changes when the moments of inertia of the solid sphere and the hollow sphere are introduced.

A solid sphere has a moment of inertia given by I = (2mr2)/5, while a hollow sphere has I = (2mr2)/3. For the hollow sphere, the conservation of energy equation becomes:

mgh = 1/2mv2 + (1/2)(v2/r2)(2mr2/3)

= 1/2mv2 + 1/3mv2

= 5/6mv2

Solving for v gives: v = (6gh/5)1/2

For the solid sphere, the conservation equation gives:

mgh = 1/2mv2 + (1/2)(v2/r2)(2mr2/5)

= 1/2mv2 + 1/3mv2

= 7/10mv2

Solving for v gives: v = (10gh/7)1/2

Thus, we can reach the same conclusion that the solid sphere will have a greater final velocity than that of the hollow sphere, but the two solid spheres will roll with the same speed since the velocity is independent of the object’s mass.

Notes:

cylinders

  • The second set of cylinders consists of three cylinders, depicted above, and identified below:
    • A: solid cylinder made from aluminum
    • B: solid cylinder made from copper
    • C: hollow cylinder partially filled with sand
    • D: hollow cylinder
  • The set of spheres consists of three different spheres, depicted above and identified below:
    • A: solid sphere composed of steel
    • B: solid sphere composed of aluminum
    • C: hollow sphere composed of steel
  • Use sandbags at the end of ramp to catch cylinders.

Written by Madison Harris