The Cycloid Ramp (or Brachistochrone Ramp) consists of three acrylic ramps; one is a straight line, one is a steep fast curve, and one is a cycloid curve. The cycloid curve is a specific curve that is found by rolling a circle and having a point on it’s edge trace the path. This curve demonstrates the fastest travel between two points.
Materials:
- Brachistochrone slot structure
- The four available brachistochrone ramps
- Three rollers
- Metal plate
- Brick
- Camera & Stand
- Metal file labeled “brachistochrone release”
Demo:
To demonstrate the phenomenon, slot in three of the four available ramps.
These ramps are:
- A very steep curve with high acceleration
- Two cycloid curves
- A straight line curve showing the shortest distance
Once the ramps are slotted, place the metal plate vertically at the base of the ramp and put the brick behind it. Now, start the rollers at the top of the ramps and release them at the same time using the metal file. The most effective way to release is to bring the rollers to the edge so they are sitting vertically, then hold the file and press them against the ramps. When ready to release, simply pull straight outwards, not upwards. The metal is there to make a loud noise when each roller strikes it, and to stop the rollers.
There are two demonstrations available with this apparatus:
Option One: To demonstrate the fastest travel between two points.
Set up the apparatus as seen in the photo (with all different curves). This will demonstrate how the roller rolling on the cycloid curve will reach the metal in the least time. Be sure to release it using the metal file in order to ensure accuracy.
Option Two: To demonstrate the cycloid curve’s nature.
Set up the apparatus with two cycloid curves adjacent to each other. Drop each roller at different heights on the curve and observe how both rollers will strike the metal at exactly the same time. You can also test this against other curves in the unused slot. Be sure to release it using the metal file in order to ensure accuracy.
For both options, it is effective to have a student (or professor) video the travel of the rollers using the ‘Slow-Motion’ option on their iPhone or Android. This makes it very clear which roller strikes the metal sheet first.
It is also effective to use the video camera and set it up from a birds-eye-view perspective, this is also very clear and can be broadcasted onto the projector screen for students to view.
Explanation:
This problem was first posed by Galileo in 1638, where he disproved the idea that the shortest distance (a straight line) would not actually be the fastest way to travel between to points. Galileo actually believed that the arc of a circle would be the fastest.
This was quickly disproved by Johan Bernoulli who posed this as a challenge to the mathematical world in 1696. Despite that Isaac Newton quickly solved this, Johan Bernoulli’s solution was incredibly clever and is described below:
Bernoulli considered what light may do to solve this problem. Since light will always take the quickest path from point A to point B. Thus, he considered, rather than a particle sliding down a chute, it is better to consider light traveling through a media of different refractive indexes as seen in Figure 1.

Figure 1. Light traveling through a media of different indexes and refracting at the boundaries. https://www.youtube.com/watch?v=Cld0p3a43fU&frags=pl%2Cwn
Due to Snell’s Law, as light moves through this index it refracts at each boundary since it’s speed changes.
where θ represents the incident and refracted angles and v represents the incident and refractive velocities.
Now, by conservation of energy, applying it back to masses rolling down a ramp:
given we denote y as the vertical axis in Figure 1.
Therefore, it becomes clear that the velocity is proportional to the square root of y. Bernoulli’s thinking was now that if Snell’s Law applies instantaneously at every boundary, what if there were infinitely many boundaries of refraction. He then questioned what that curve would be.
Applying Snell’s Law again:
where k is some constant number.
This was recognized by Bernoulli as the differential equation of a curve of the cycloid. A cycloid is the curve traced by the point on a edge of a rolling circle, as seen in Figure 2.
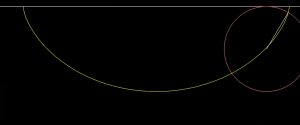
Figure 2. Cycloid curve (in yellow) with a rolling wheel (in red). https://www.youtube.com/watch?v=Cld0p3a43fU&frags=pl%2Cwn
Notes:
- It is likely you will need to bring a cart as the apparatus is heavy and has many parts.
- A camera is recommended so that there is an option to show the video to see which roller strikes the metal first.
Written by Phoenix Gallagher
