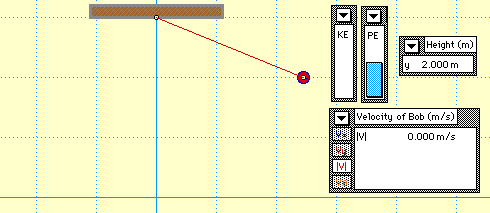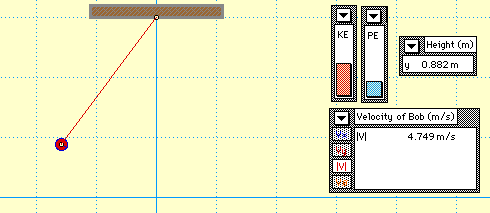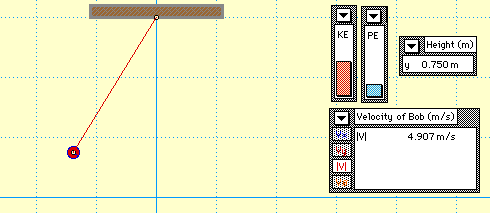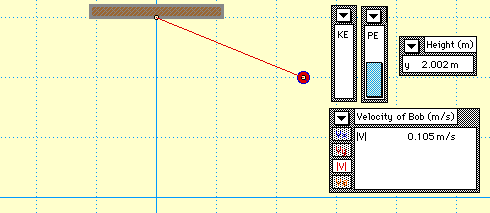
This is an exciting and popular demonstration and shows conservation and transformation of energy for a pendulum. Two setups are available.
Thimann 3
Setup: A modified bowling ball with a hook mount is attached to a cable from the ceiling (Thimann 3 is the only classroom to have the cable).
Procedure: The instructor leans against the wall while holding the bowling ball close to his/her face. The supporting cable, attached to the ceiling, has to be tight. Then, he/she carefully releases the ball and stays without fear as the bowling ball makes the full swing, returns back, and stops millimeters from his/her face. Brave students can try this too!
All other locations
Setup: A modified bowling ball with a hook mount is attached to a cable hanging from a board clamped between two ladders.
Materials:
- Two 8-ft tall ladders (one can be borrowed from the campus woodshop)
- Bowling ball with hook mount
- Board with eye hook and cable attached
- Two large clamps to secure the board to the ladders
- Two volunteers to stand on the ladders for extra stability during the demo
Procedure: The instructor stands behind the ladders while holding the bowling ball close to his/her face. The supporting cable, attached to the board, has to be tight. Then, he/she carefully releases the ball and stays without fear as the bowling ball makes the full swing, returns back, and stops millimeters from his/her face. Brave students can try this too!
Explanation
In a closed system with no energy lost to friction (from either air resistance or friction between surfaces), there are only two forces that act on the pendulum. The first force is gravitational force, 
The other force that acts on the pendulum is the tension force pulling up on the bowling ball. This is not an internal or conservative force so it can change the total mechanical energy of the bowling ball. However, because the force of tension always acts perpendicular to the direction of motion, and
we can see that the work done by the tension will be zero. This is because 
At its highest points, the pendulum will be momentarily motionless. This is because at these points, all of the kinetic energy has been transformed into gravitational potential energy. Conversely, when the pendulum is at the bottom of the arc, its potential energy is zero and it has the highest velocity of any point. Even though the mechanical energy of the system is transformed throughout the period of the pendulum, the total mechanical energy stays constant throughout the cycle, which means that as it is released, the potential energy that it loses is changed over entirely to kinetic energy.
This demonstration also shows conservation of energy. If this were a perfect system where no energy was lost to friction, the amplitude of the pendulum would stay constant for as long as it was swinging. While this pendulum is almost a perfect system, there is still some energy that is lost to air resistance opposing the direction of motion of the bowling ball and friction of the knot attaching the pendulum to the board. This means that we have a damped system and eventually the pendulum will come to rest. Because there is some energy lost in the system, it is a fun demo to release the bowling ball very close to your face or stomach and watch it come back to within millimeters of where it was released (as long as you don’t move!).
Both air resistance and the friction in the knot are friction forces, which serve to translate kinetic energy into heat. However, even though there is energy being turned into heat on the surface of the bowling ball and in the rope, it is unlikely that you would be able to feel the difference in temperatures because the change will be so small.
Notes
- Please request this demo at least three days in advance so we can obtain the ladder from the woodshop.
- This demo requires 2-3 people to set up
- No one should ever stand more than one rung above the ground on the ladders
Written by: Sophia Sholtz