Equipment:
- Pulley
- 2 Masses of different weights (~200g-1kg)
- Pegboard
- Waxed string (this helps prevent the string from slipping off the pulley)
Demo:
This is a commonly used apparatus to demonstrate the principles arising from classical mechanics. The machine itself consists of two masses, usually denoted by m1 and m2 connected by a massless string that is draped over a massless, ideal pulley. This is depicted in Figure 1. When m1 is equal to m2, the system is in equilibrium and neither mass experience acceleration. If the masses are not equal, they will both experience equal acceleration.
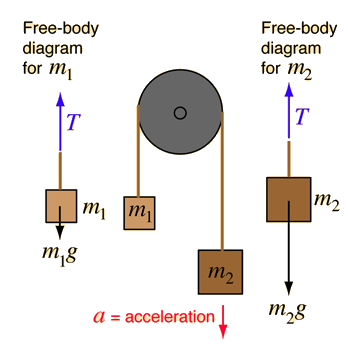
Figure 1: Atwood machine with free body diagrams for m1 and m2. Image courtesy of HyperPhysics.
Explanation:
The weights of the masses attached to the string that is draped over the pulley are significantly greater than the mass of the pulley and the string. This means that we make the assumption the both the pulley and the string are ideal massless components.
Because we’ve assumed that the mass of the string and the mass of the pulley are negligible, as well as the effects of friction, we may say that the force of tension acting on each mass is equal in magnitude. We may now apply Newton’s second law to each object.
For m1, we have:
Knowing that a1 will be in the positive direction, we may rewrite the above equation to say:
For m2, we have:
This time, we know that the a2 will be in the negative direction, so if we denote this as -a, we may rewrite our equation to say:
Now, we may subtract from
to obtain:
We can sub in numerical values for and
. Let
,
. Then the equation for
becomes:
This is what we expect. Since the second mass is heavier, it will move in the negative direction, while the first mass will move upwards (positive).
It is quite easy to see the opposite scenario; when the first mass moves downwards. All that needs to happen is for the first mass to be heavier than the second mass. Let and
. Then we have the following:
Clearly, the first mass will move downwards (in the negative direction).
Notes:
- String tends to slip off of pulley if pulled too quickly
Written by Madison Harris