The use of Gauss’s law to examine the electric field outside and inside of a charged conducting sphere sometimes does not convince students that there is no electric charge or field inside the sphere. This demonstration is designed to show students that this is the case.
Materials:
- Van de Graaff generator with discharge rod
- Insulated hollow aluminum sphere with hole on top
- Gold leaf electroscope
- Small metal probe attached to a long plexiglass rod
Demo:
Ensure that the electroscope and discharge rod are grounded. Connect hot wire from the Van de Graaff generator to the metal sphere, as shown in figure 1. Turn the Van de Graaff generator on for five to ten seconds to charge the insulated sphere.
Use the metal probe to tap the outside of the insulate sphere, and then tap the metal cap on top of the electroscope. The electroscope should detect some electric charge, identified by movement of the gold leaf.
Discharge the electroscope. Now touch the inside of the insulated sphere with the metal probe, careful not to touch any edges on the way in and accidentally giving the probe some charge from the outside of the sphere. Carefully remove the probe, and test it again using the electroscope. The gold leaf should stay in place, indicating that there is no electric charge inside of the sphere.
Discharge the Van de Graaff generator using the discharge rod before handling to prevent electric shock.
Explanation:
Some definitions:
- Q = Total charge on our sphere
- R = Radius of our sphere
- A = Surface area of our sphere =
- E = Electric Field due to a point charge =
- ε = permittivity of free space(constant)
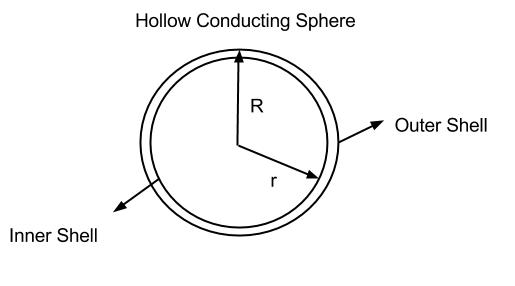
Electrons can move freely in a conductor and will move to the outside of the sphere to maximize the distance between each electron. There is more surface area on the outside of the sphere than on the inside, so the electrons travel to the outside to have more space between one another, as like charges repel.
Using figure 2, we can see that the radius extending from the center of a cross-section of our sphere to the inner shell is smaller than the radius extending to the outer shell. The surface area is proportional to the radius squared, so this means that the outer shell has a larger surface area.
Now that we know that electrons will tend to move to the outside of the hollow sphere, let’s examine the electric field inside and outside of the sphere.
Guass’ Law states that the total electric flux(equation below) through a Gaussian surface is equal to the charge enclosed by the surface divided by the permittivity of free space. Electric flux can also be defined by the electric field multiplied by the surface area of the Gaussian surface:
This law also implies that a point charge with charge Q contained in a Gaussian surface and a surface with a total charge Q contained in the same Gaussian surface have the same electric flux. This means that we can treat surfaces like a point charge, simplifying calculations.
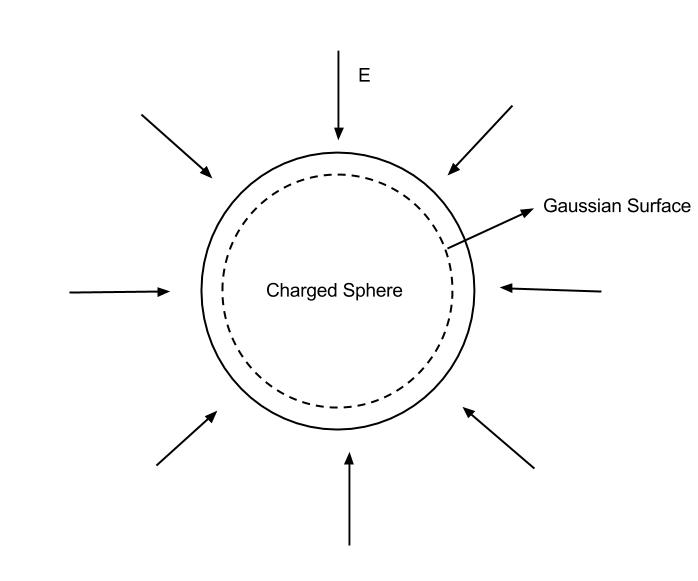
Let’s look at our case, with negative charge distributed about the shell of a hollow sphere. We want to know what the electric field is inside and outside of the sphere. Using Gauss’ Law, we can examine the electric flux and field inside of the sphere imagine a Gaussian sphere just inside barely inside or on top of our charged sphere(figure 3).
As no charge, Q, is contained within the hollow part of our sphere, the net flux through our Gaussian surface and electric field are both zero inside of the sphere.
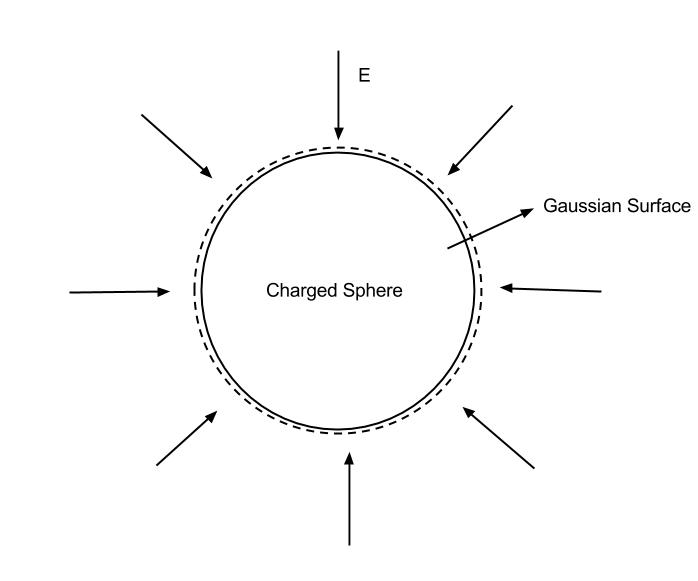
To examine the electric flux and field outside of the sphere, let’s imagine our Gaussian surface just outside of our charged sphere. Now the Gaussian surface contains all of the charge on the surface of our hollow sphere, and we can treat this entire shell as a point charge with a charge of Q(figure 4).
This means that there exists some electric flux and electric field outside of our conducting sphere:
Notes:
Use of video camera recommended for a large audience.
Written by Lydia Seymour