Materials:
- Scale on a stand
- Plastic cylinder with a nozzle, filled with dyed water
- Empty glass to collect displaced water
Part one:
- Red pool ball attached to a plastic cup by a string
- Gray pool ball on a string
Part two:
- Set of weights
- Hollow copper sphere attached to a plastic cup by a rigid wire
- Empty plastic cup with three strings
Procedure:
- Carefully zero scale on the stand.
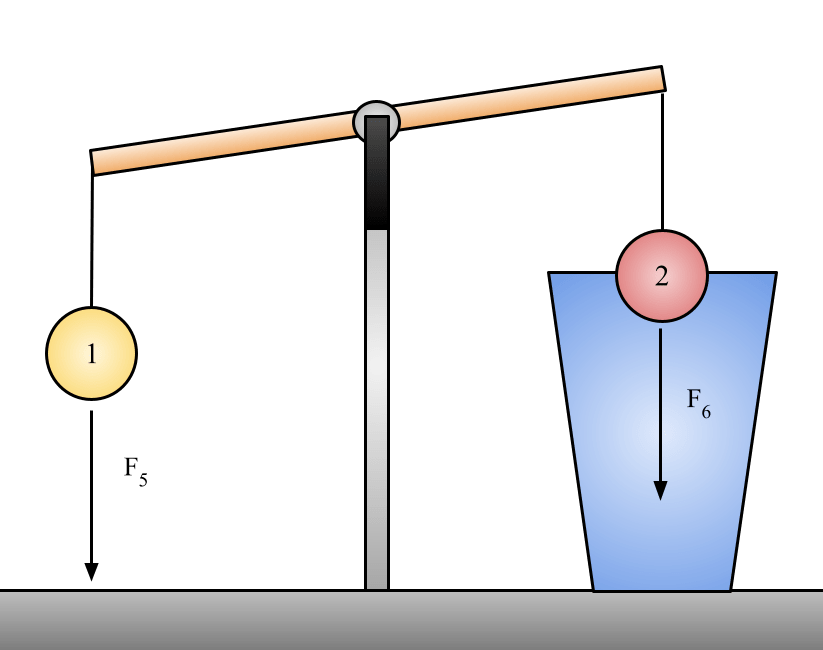
- Show the students that the weight of the red ball and cup on one side of the scale is equal to the weight of the gray ball on the other side (Pic 1).
- Detach the gray ball from the scale and then allow the red ball to sink into dyed water. Collect all displaced water in the empty glass (Pic 2).
- Reattach the gray ball to the scale and pour collected displaced water into the cup (Pic 3).
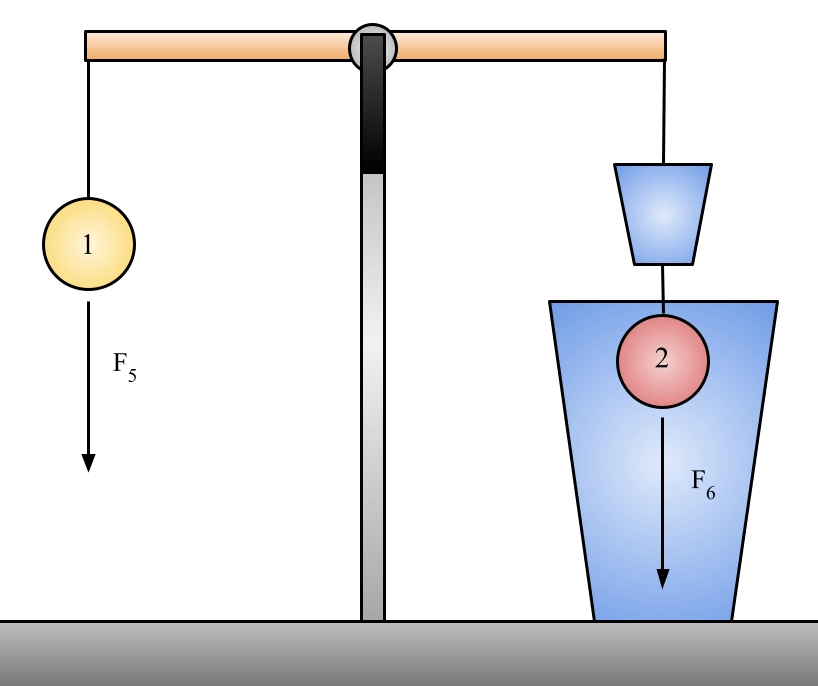
- Show the students that the submerged red ball with water in the cup is in equilibrium with the gray ball (Pic 4).
Explanation:
This part of the demo shows that the weight of the displaced water is equal to the buoyant force acting on the red ball. When both the red and grey balls are on the scale and the red ball is placed in water and allowed to come to equilibrium, we see that it does not sink completely into the water, but rather floats on top of the water in the container. Because we can see the red ball floating on the water, we know that it must be experiencing some buoyant force that causes the effective weight of the red ball to be less than the effective weight of the grey ball.
We can show that the weight of the displaced water is equal to the buoyant force by adding the displaced volume of water to the cup above the red ball. Once this additional mass is added, the red and grey balls are equal weights on the scale (shown by the scale balancing itself).
Following are force diagrams showing the forces acting in each of the three situations that happen above:
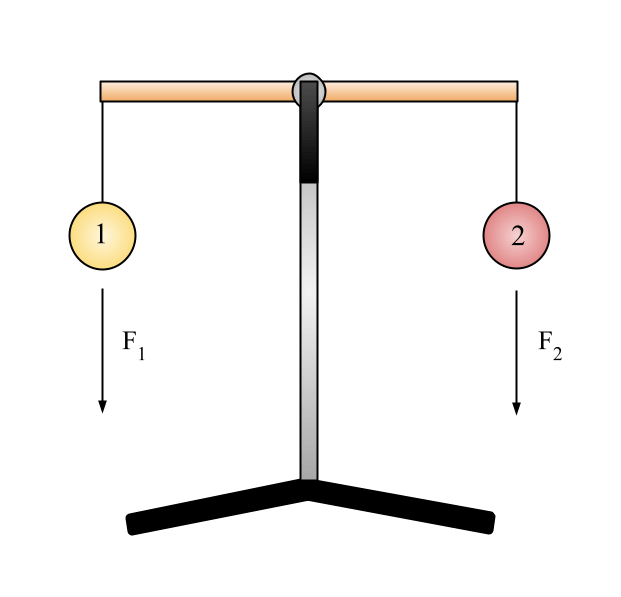
This depicts the forces F1 and F2 when neither of the balls are submerged in water. We know that mass 1 equals mass 2, allowing us to calibrate the scales appropriately.
We know (according to Newtons Second Law) that F = ma. We can describe the forces F1 and F2 as follows:
F1 = -m1a
F2 = -m2a
Where m1 is the mass of the grey ball and m2 is the mass of the red ball and cup. Here we assume that the plastic cup adds a negligible amount of weight, and it is comparable to the weight of the string on the grey ball. The force is negative because I defined any force acting in the downward direction as a negative force (but know that you can define a negative force acting in the positive direction and you should get the same result) and a is the acceleration due to gravity (9.8m/s2). We know that the two spheres are equal in mass, and that the acceleration due to gravity will not change based on position. This means that F1 = F2. We can see this visually because they balance on the scale.
We know that m1 and m2 are equal in weight, but in this part of the demo we see that the forces acting on them cannot be equal. We know this because the scale is no longer balanced, and the grey ball (ball 1) appears to have a much larger effective weight than the red ball (ball 2). F1 and F4 are the total forces acting on balls one and two, respectively.
F3 = -m1a ,F3 =F1
F4 = -m2a + Fb
Where Fb = the buoyant force acting on the ball. We know there must be a force acting on the second ball because the scale no longer reads that the two balls are equal weights.
We know that the two total forces, F5 and F6 must equal one another because the scale is once again balanced. This will come into play in a few lines. Before then, lets look at the individual forces contributing to the total force that each of the balls feel.
F5 = -m1a = F1
Once again, the force on the grey ball is just equal to the mass of the ball multiplied by the force of gravity. However, the red ball (ball two) is very interesting in this case.
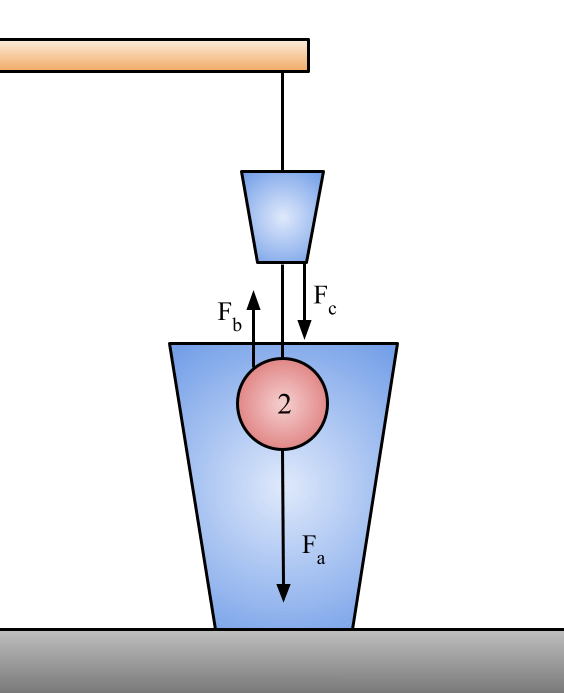
Fa = -m2a, Fb = the buoyant force, and Fc = -mda, where md is the mass of the displaced water that we caught in a cup
F6 = Fa + Fb + Fc = -m2a + Fb– mda
In the figure above, Fa = -m2a, Fb = the buoyant force, and Fc = -mda, where md is the mass of the displaced water that we caught in a cup. Because the scale is once again balanced, we know that the total forces acting on each of the balls must be equal, F5 = F6.
From that, we can set
F6 = -m2a + Fb– mda = -m1a = F5
We know that m1 = m2, so we can remove those two terms from the sum to get:
Fb – mda = 0
Fb = mda
And we can see that the buoyant force felt by the red ball is equal to the weight (the force) of the displaced water.

Part 2
Demo:
- Hang an empty cup on left side of the scale. On the other side hang the cup with a hollow metal sphere attached by a rigid piece of wire. Slowly add weights into the left cup until the scale is in equilibrium (Pic 1).
- The amount of weight added should be equal to the weight of the hollow metal sphere – approximately 41g (Pic 2).
- Force the hollow metal sphere to submerge by holding the wire and pushing it downward. Collect all displaced water in the empty glass (Pic 3).
- Remove the weights from the left cup and pour collected displaced water into it. Show the students that the weight of the displaced water is much greater than the weight of the hollow metal sphere (Pic 4).
Explanation:
The explanation for this part again has to do with Archimedes’ principle, but it shows that the weight of displaced water doesn’t necessarily equal the weight of the object if it is being forced under the water. The weight of the displaced water will equal the weight of the hollow metal sphere if they are allowed to come to equilibrium and the hollow sphere is allowed to float on top of the water. If the metal sphere is forced under the water, the amount of water displaced is equal to the sphere’s volume. Since the water is denser than the hollow sphere, the weight of the water displaced will be more than the weight of the sphere, even if they are displacing the same volume. You can think about it like a basketball and a bowling ball. They both displace the same (roughly) volume of air, but they weigh very different amounts because they don’t have the same density.
Note:
Plastic cylinder has to be filled up to the nozzle level.
Written by Sophia Sholtz