Materials:

• Inertia Demo box, shown Figure 2 [Cabinet A2]
  • 2x 1kg masses
  • 2x long rods for handles
  • Thick (but easily breakable) cotton string
• 2x bases
• 3x rods
• 2x 90° clamps
• Thick gloves [Cabinet B3]
• Sand bags for padding the desk and securing the base of the stands [Cabinet A3]

 

Demo:

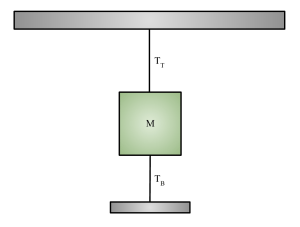
Two equal weights are suspended by string, while two more strings hang below them with long rods for handles. When the handle is pulled down with a jerk, the lower string breaks, but when it is pulled with an even force, the upper string breaks.

Explanation:

This demo displays Newton’s First Law (an object at rest will stay at rest unless acted upon by a force) and Second Law (F=Ma) of Motion, and can be explained using either. Using Newton’s Second Law requires more math than simply explaining it with inertia, but can provide interesting insight into the actual physics at play.

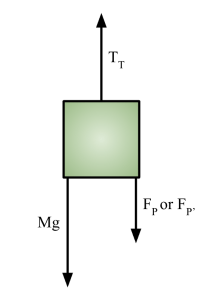
• T_T = tension on the top string
• F_P or F’_P = force with which person is pulling on the bottom string
• Mg = weight of mass M (assume massless string)

The tension of the top string is due to the weight of the mass (initially, with no one pulling):  T_T = Mg

The tension of the bottom string is initially 0 (with no one pulling–we assume that the little rod is massless): T_B = 0

There is a critical tension force T_C at which the string breaks.

CASE 1

The person pulls slowly on the handle with force F_P
There is plenty of time for the weight to feel F_P

Tensions:

• T_T = F_P + Mg
• T_B = F_P

At the point F_P + Mg = T_C, the top string will break (T_T > T_B always for this case)
The total force the person must exert is F_P = T_C – Mg

CASE 2

The person pulls quickly on the handle with force F’_P (downwards)
There is not enough time for the weight to feel F’_P

Tensions:

• T_T = Mg
• T_B = F’_P

At the point F’_P = T_C, the bottom string will break. The magnitude of T_C required is the same as in Case 1, where T_C = F_P + Mg. The total force the person must exert now is F’_P = F_P+Mg (the weight of the mass is no longer “helping” them attain the critical tension force)

The top string never feels the force F’_P, and thus never gets to the critical tension.

The inertia of the mass is relatively large, so the mass will resist any movement.

The string here is somewhat elastic, and can be thought of as a spring. Think of hooking a spring to an elephant on an ice rink. If you pull on the other end of the spring, it will take time for the spring to stretch and eventually move the elephant; we say the elephant has a lot of inertia. If instead of an elephant, we hook up a mouse and pull on the spring, the mouse will start moving almost immediately (the spring does not stretch as much). The mouse has much less inertia, and resists motion significantly less than the elephant.

————————————————————————–

THE FOLLOWING EXPLANATION IS INCORRECT but is commonly found on the internet. It may be helpful to understand why it is incorrect in case there are questions pertaining to this ‘explanation’.

————————————————————————–

Using Newton’s Second Law of Motion:

F_NET = Ma

For F_NET (the net force in the y-direction), we take into account the forces that are acting on the weight, M. This gives us

T_B + Mg – T_T = Ma

Where a is the acceleration with which the weight is pulled down by the person, and g is the acceleration from gravity. Acceleration is defined as positive in the downward direction.

Rearranging, we get:

T_B – T_T = Ma – Mg

T_B – T_T = M(a-g)

 

CASE 1

When the weight is pulled down slowly, with the acceleration much smaller than that of gravity:

a < g

M(a-g) < 0

T_B – T_T < 0

T_B < T_T

If you are accelerating down much less than the acceleration due to gravity, the tension on the bottom string is much less than the tension of the top string*. Because the tension is greater at the top, that string will break first.

*As a→0, T_T = T_B + Mg

CASE 2

When the weight is pulled down quickly, with the acceleration much greater than that of gravity:

a > g

M(a-g) > 0

T_B – T_T > 0

T_B > T_T

This means that the tension on the bottom string is greater than the tension on the top, so the bottom string will snap first.

————————————————————————–

Again, the explanation given above is NOT why the top string breaks with a slow, even force and why the bottom string breaks with a fast pull. While this appears to be a clean explanation which makes sense of what happens, there are two main problems.

The first problem is that it isolates the acceleration of the bottom string and handle (a) from the total acceleration felt by the system (g). We know that these two accelerations are related and cannot be separated so easily.

The second problem with this solution (and the most easily identifiable with a control experiment) is that the math is independent of the mass and its placement along the string. This equation separates the tension in the bottom string from the tension in the top string, but does not explain why the tension difference would only happen if there was a mass present, dividing the string. Theoretically, this means that the equation should still hold true if no mass were present (there was just one string with a handle), where the tension in the top string is equivalent to tension in the upper part of the string and the tension in the bottom string is equivalent to the tension in the lower portion of the same string. This means that if you repeated the experiment with one piece of string and no weight, pulling quickly would lead the string to break near the bottom and pulling slowly would lead the string to break at the top.

When this control experiment was done, we found that this did not occur. The string broke near the bottom the vast majority of the time*, independent of how quickly we pulled the string.

Because we could not show that the tension was directly related to the distance from where the force was applied, we have to discount this solution in its entirety. We believe the best explanation can be given by assuming the string has a measurable (but very small) spring coefficient, which becomes apparent with a large mass. This is explained most simply by the elephant and ice rink example near the top of the page.

*there were a few times the string broke near the top but we believe that to be more correlated with intrinsic weak points in the string rather than any major differences in tension as a function of x (distance from the point where force was applied), furthermore, we could not reliably replicate the string breaking near the top, leading us to believe it is an anomalous event.

Notes:

• Grab handles with two hands on either side of rod so your fingers are not below the falling path of the weight.
• Watch fingers!!!
• Put the sand bags below where the weight will fall (below the even force weight) so as to not damage the desk.
• Tie knots for two extra lengths of string in case one pull breaks the wrong section of string

Written by Sophia Sholtz