Friction – Static and Kinetic | UCSC Physics Demonstration Room

Version 1: Friction Carts and Force Sensor

There are three different types of friction carts, or trays, with felt, cork and plastic on the bottom….

List of Parts:

Plastic PASTrack
Friction Carts (Felt, Cork and Plastic Bottom)
Wireless Force Sensor
String

Explanation:

Finding the Coefficient of Static and Kinetic Friction

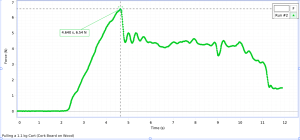
Figure 1: Plot depicting the force of pulling a 1.1 kg (cork board on wood) cart over time.

As the friction cart moves across a flat surface, the force sensor will record the frictional force as a function of time, creating a graph that shows the frictional force reaches a maximum before decreasing. Figure 1 shows an example of a graph that will be created. By repeating this demonstration multiple times, each with a different mass in the cart, it will be possible to obtain a frictional force versus normal force plot.

By remembering the two equations for static and kinetic frictional forces,

$F_s = {\mu}_sN$ (static friction)

$F_k = {\mu}_kN$ (kinetic friction),

The slope of the static frictional force versus normal force graph will give the coefficient of static friction, while the slope of the kinetic frictional force versus normal force graph will give the coefficient of kinetic friction. By using different masses in the cart, the normal force changes as well. This is according to the equation

$F_N = Mg$ .

If a flat surface was used, then that equation can be applied, since the normal force will only be acting against the weight of the mass, which in this case is Mg. As such, the plots can then be created to find the two coefficients of friction.

Work Done by Friction

Work done is equivalent to the change in kinetic energy of an object. First, determine the velocity of the cart without any additional masses. Next, the cart with an additional mass can be launched towards a motion sensor to demonstrate that the mass would cause sliding friction, resulting in the cart decelerating at a constant pace. By measuring how far the cart slid before coming to a stop, all the necessary information has been collected to calculate the coefficient of friction using the following equation:

$\frac{1}{2}mv^2 = {\mu}_kF_Nx$

$\frac{1}{2}mv^2$ = kinetic energy
${\mu}_k$ = coefficient of kinetic friction
$F_N$ = normal force
$x$ = distance

Once again, the normal force will be equivalent to the weight of the cart and mass if pulled across a flat surface.

Version 2: Multi-Surfaced Cube with Weights

Friction cube balanced by a weight

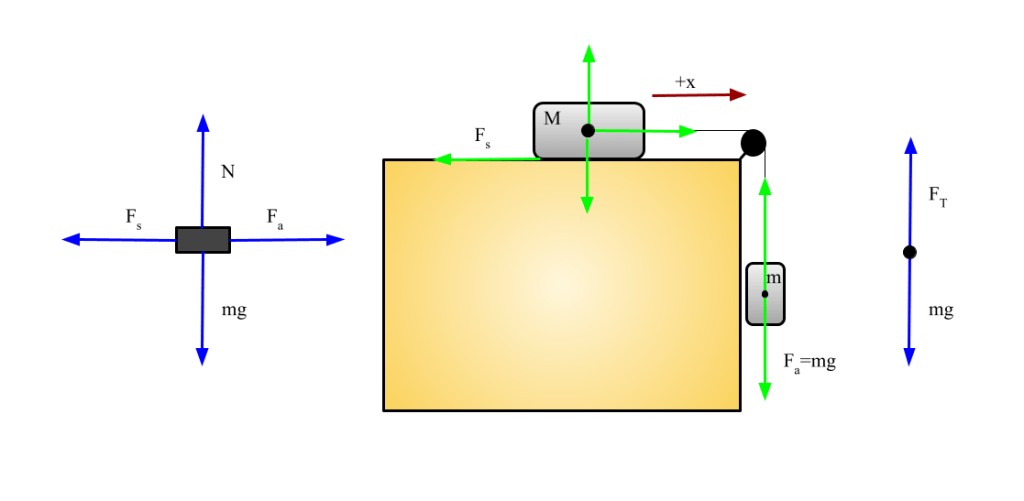
A wooden cube with cork, aluminum and sandpaper surfaces is dragged across a wooden plane by weights suspended over a pulley. (top). Add weight slowly until static frictions is overcome and the block is in constant motion. Do this for each surface and compare results.

List of parts:

Multi-surface cube with string
Wooden plane with pulley
Set of weights and hanger for weights

Explanation:

List of kinetic friction coefficients for the block surfaces and wood:

screen-shot-2016-10-18-at-16-03-43

This demonstration is useful primarily to demonstrate static friction. The block usually starts accelerating too quickly once it begins to move, and it is hard to quantify the kinetic friction coefficient.

This demonstration does a good job at showing the friction coefficients for different materials that cover the block. Because sandpaper on wood has a higher static friction coefficient than wood on wood and aluminum on wood, it will take a greater force to move the sandpaper on wood than for either of the other two sides.

The force required to begin moving the block is equal to:

$F_s = {\mu}_sN = F_a$

F_s = force of static friction
μ_s = static friction coefficient of the two materials in contact with one another
N= normal force (force perpendicular to the contact surface)
F_a = Applied force

Because the mass is supported on the table (not undergoing any change in direction on the y-axis), we can say

$N = Mg$

The applied force on the block is approximately equal to the tension force in the string. The force felt by the weights themselves is F_a = mg – F_T because, in addition to F_T pulling upward, gravity is pulling down on the weight. Because the block and the weight are connected by the string, they will have the same acceleration, a.

Thus, the force required to begin moving the block is:

$F_a > Mg{\mu}_s$

If F_a = F_s, the forces in the system are balanced and the block does not move. However, as soon as the applied force is greater than the force of static friction, the block will have a force acting on it in the +x direction.The magnitude of this force is

$F_T = F_a - F_s$

F_s is a changing force, and will match the applied force until the applied force exceeds the possible static force, given by the weight of the object and the static friction coefficient of the materials interacting.

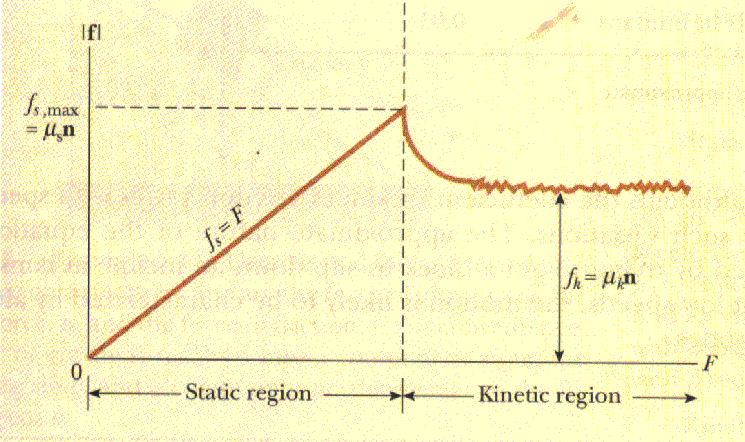
Source: http://www.ux1.eiu.edu/~cfadd/1150/04Nwtn/frict.html

This graph shows the increasing quantity of F_s with the increasing F applied, before F_s reaches its maximum value and the block begins moving.

Version 3: Observing Static and Kinetic Friction with Lead Bricks

A lead brick attached to a Newton scale is pulled slowly with increasing force until static friction is overcome so that the brick is in constant motion. Take note of the Newton scale before (left) and after the moment the brick begins to move (right).

List of parts:

Two lead bricks with hooks and wooden base
Wooden plane
Newton Scale with string attached (use Newton scale that goes up to 50N, not 20N (else the bricks max out the scale))

Explanation:

This demo shows the difference between the static friction coefficient and the kinetic friction coefficient. The static friction coefficient is always greater than the kinetic friction coefficient, meaning it will take a greater force to begin to move the block than it will to continue to accelerate the block once it has begun moving.

In this demo you will pull the Newton scale with increasing force until F_a > F_s, when the block begins to move. At this point, in order to keep the block moving at a constant speed, you will only need to apply a force equal to that of the friction force experienced by the block.

Notes:

With lead blocks make sure the wood track doesn’t start slipping on the tabletop before the lead bricks start slipping on the wood track, else you will measure the force required to overcome the static friction coefficient of the track on the tabletop.

Written by Sophia Sholtz